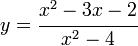domingo, 28 de abril de 2013

función racional

En matemáticas, una función racional es una función que puede ser expresada de la forma:

f(x) = \frac{P(x)}{Q(x)}

donde P y Q son polinomios y x una variable, siendo Q distinto del polinomio nulo. Las funciones racionales están definidas o tienen su dominio de definición en todos los valores de x que no anulen el denominador.1

La palabra "racional" hace referencia a que la función racional es una razón o cociente (de dos polinomios); los coeficientes de los polinomios pueden ser números racionales o no.

Las funciones racionales tienen diversas aplicaciones en el campo del análisis numérico para interpolar o aproximar los resultados de otras funciones más complejas, ya que son computacionalmente simples de calcular como los polinomios, pero permiten expresar una mayor variedad de comportamientos.

RationalDegree2byXedi.gif
Función racional de grado 2:
y = \cfrac{x^2 -3x -2}{x^2 -4}
RationalDegree3byXedi.gif
Función racional de grado 3:
y = \cfrac{x^3 -2x}{2(x^2 -5)}
Publicado por en No hay comentarios:

teorema de factorización

FACTORIZACIÓN DE POLINOMIOS

 

Para factorizar polinomios hay varios métodos:

 

  1. Sacar factor común: Es aplicar la propiedad distributiva de la multiplicación respecto de la suma, Así, la propiedad distributiva dice:

 


 

Pues bien, si nos piden factorizar la expresión , basta aplicar la propiedad distributiva y decir que

 


 

Cuando nos piden sacar factor común o simplemente factorizar y hay coeficientes con factores comunes, se saca el máximo común divisor de dichos coeficientes. Por ejemplo, si nos piden factorizar la expresión , será

 


donde 6 es el máximo común divisor de 36, 12 y 18

Para comprobar si la factorización se ha hecho correctamente, basta efectuar la multiplicación, aplicando la propiedad distributiva de la parte derecha de la igualdad, y nos tiene que dar la parte izquierda.

 

Otro ejemplo: Factorizar

 

 ¡Atención a cuando sacamos un sumando completo!, dentro del paréntesis hay que poner un uno. Tener en cuenta que si hubiéramos puesto  y quiero comprobar si está bien, multiplico y me da  pero no  como me tendría que haber dado.

Sin embargo si efectúo

 

Otros ejemplos:

 



 

  1. Si se trata de una diferencia de cuadrados: Es igual a suma por diferencia.

Se basa en la siguiente fórmula

 


 

Pero aplicada al revés, o sea que si me dicen que factorice  escribo

 


Otros ejemplos de factorización por este método:

 




 

  1. Si se trata de un trinomio cuadrado perfecto: Es igual al cuadrado de un binomio

Se basa en las siguientes fórmulas

 

   y   

 

Así si nos dicen que factoricemos: , basta aplicar la fórmula anterior y escribir que

 

Publicado por en No hay comentarios:

teorema fundamental del algebra

El teorema fundamental del álgebra establece que todo polinomio de una variable no constante con coeficientes complejos tiene un raíz compleja, es decir, existe un número complejo que evaluado en el polinomio da cero. Este incluye polinomios con coeficiente reales, ya que cualquier número real es un número complejo con parte imaginaria igual a cero.

Aunque ésta en principio parece ser una declaración débil, implica todo polinomio de grado n de una variable no constante con coeficientes complejos n tiene, contando con las multiplicidades, exactamente n raíces. La equivalencia de estos dos enunciados se realiza mediante la división polinómica sucesiva por factores lineales.

Hay muchas demostraciones de este importante resultado, que requieren bastantes conocimientos matemáticos para formalizarlas. El nombre del teorema es considerado ahora un error por muchos matemáticos, puesto que es más un teorema del análisis matemático que del álgebra.
Publicado por en No hay comentarios:

teorema del factor y del residuo

Teorema que establece que si un polinomio de x, f(x), se divide entre (x - a), donde a es cualquier número real o complejo, entonces el residuo es f(a).
Por ejemplo, si f(x) = x2 + x - 2 se divide entre (x-2), el residuo es f(2) = 22 + (2) - 2 = 4. Este resultado puede volverse obvio si cambiamos el polinomio a una de las siguientes formas equivalentes:
f(x) = (x-2)(x+3) + 4
Como se muestra, la expresión anterior nos puede llevar fácilmente a esperar que 4 sea el residuo cuando f(x) se divide entre (x-2).
El teorema del residuo nos puede ayudar a encontrar los factores de un polinomio. En este ejemplo, f(1) = 12 + (1) - 2 = 0. Por lo tanto, significa que no existe residuo, es decir, (x-1) es un factor. Esto puede mostrarse fácilmente una vez que reacomodamos el polinomio original en una de las siguientes expresiones equivalentes:
f(x) = (x-1)(x+2)
Como se muestra, (x-1) es un factor.
Publicado por en No hay comentarios:

ceros y raices de una función

CORTES CON EJE ABSCISA (x). CEROS DE UNA FUNCIÓN
  En el eje de abscisa o eje de coordenadas X, se representan los originales que tienen imagen, es decir, que pertenecen al dominio de F(x). Cuando para un x determinado (x = a) se cumple que F(a) = 0, o lo que es lo mismo, los originales que tienen por imagen al número cero, se dicen que son puntos de corte con el eje abscisa o x. Recuerde que este eje es una recta de ecuación y = 0 (F(x) = 0).
  Se dice que x es punto de corte con el eje X si:
F(x) = 0.
Polinomios.
  Se debe, si se puede, factorizar para encontrar los valores que hacen y = P(x) = 0. Raices.
P(x) = x3 - 6·x2 + 9·x = x · (x - 3)2 = 0  que se anula para x=0 y x=3 >> P(0)=0 y P(3)=0. Luego hay dos puntos en esta función que están sobre el eje x: (0 , 0) y el (3 , 0).  Ver
Racionales.
  Es muy común el error, cuando tenemos una expresión del tipo:
 
 n(x)
       n(x) numerador
C(x) =  
————
  = 0    
 
 d(x)
       d(x) denominador
pasar d(x) multiplicando a la derecha de la igualdad, multiplicando al cero y resolver la ecuación n(x) = 0. Si un x = a cumple que n(a) = 0 pero también que d(a) = 0 entonces, x = a,  no es cero de la función C(x). No se verifica que C(a) = 0.
  Para que lo sea tiene que cumplirse que n(a) = 0 pero d(a) ≠ 0. Recordar que (0/k)=0 si k ≠ 0.
  En un caso práctico, se resuelve n(x) = 0 y las soluciones se sustituye en d(x), excluyendo como ceros aquellos que anulen la función denominador : d(a) = 0.
  Vimos que no se puede dividir por cero. Si ese valor anulase el denominador, ese valor no pertenecería al dominio de la función, no pudiendo tener al número cero como imagen.
Para que x = a sea punto de corte con el eje x se debe cumplir:
C(a) = n(a)/d(a) = 0  »  n(a) = 0 y d(a) ≠ 0
Valores que anulen el numerador y no el denominador
Por ejemplo:
 
 (x - 1)·(x - 3)
       n(x) numerador
C(x) =  
——————
  = 0  
 
 (x2 - 1)
       d(x) denominador
x = 1 y x = 3 anulan al numerador, pero sólo x = 3 anula al numerador y no al denominador. Esta función corta al eje x en (3 , 0). El valor x = 1 queda excluido por anular, simultáneamente, al numerador y denominador. Observe como en x = 1 tiene un punto de discontinuidad evitable. No existe C(1). No pertenece al dominio.
Exponencial.
  Si intentamos resolver F(x) = e-x comprobaremos que e-x ≠ 0 porque e-x > 0 para todo x. Ver
Logaritmo.
Log f(x) = 0 si     f(x) = 1   ya que Log 1 = 0.
Log (x + 2)  ►   x + 2 = 1  ►   x = -1  Ver
Log (x2 - 4)  ►   x2 - 4 = 1   ►   x2 = 5  ►    x = ±5(1/2)  (raíz cuadrada de 5). Ver
Trigonométrica.
sen (x) = 0  si   x = múltiplo de π, es decir  x = k·π   con k entero (Z). Ver
cos (x) = 0  si  x = multiplos de π más la mitad de π;   x = (π/2) + k·π  con k entero (Z). Ver
tan (x) = 0 donde sen (x) = 0 ya que tan (x) = sen (x) / cos (x). Seno y coseno no se anulan simultáneamente. Ver
 
  Por ejemplo, para la función vista arriba
  p(x) = -x4 + x2 = x2·(1 - x2) = 0  ►   x = 0  y  x = ± 1.
  Su dominio es R.
Publicado por en No hay comentarios:

modelo general de funciones polinomiales


Publicado por en No hay comentarios:

sábado, 27 de abril de 2013

funcion de grado 4

Publicado por en No hay comentarios:

division sintetica

La división sintética es un procedimiento "abreviado" para determinar el cociente y el residuo que se obtiene al dividir un polinomio $P(x)$ de grado $n, \, \, \, n \geq 1$, por un polinomio de la forma $x-\alpha$, con $\alpha \in I \!\!R$, a partir de los coeficiente de $P(x)$ y el cero de $x-\alpha$.

El procedimiento que usaremos para realizar la división sintética de un polinomio $P(x)$, por un polinomio de la forma $x-\alpha$, lo ilustraremos a través de ejemplos.
Ejemplo:

Sean $P(x)$ y $Q(x)$ polinomios tales que:

$P(x) = 4x^3+3x^2-5x+2; \, \, \, \, Q(x) = x-3$

Determine el cociente y el residuo que se obtiene al dividir $P(x)$ por $Q(x)$:

a) Usando el método estudiado anteriormente (División larga)

b) Usando división sintética


Solución:

a)



Por lo que al dividir $P(x)$ por $Q(x)$ se obtiene $4x^2+15x+40$ como cociente y 122 como residuo.

b) Usando división sintética, $P(x)$ se divide por $Q(x)$ de la siguiente manera:

Donde los números 4, 15 y 40 son los coeficientes del cociente y 122 el residuo de la división.
Observe que, según la parte (a) de este ejercicio, los números obtenidos en la tercera fila son los coeficientes del cociente y el residuo, como se muestra en el esquema anterior.
Los números representados en la primera fila son los coeficientes de $P(x)$ (dividendo) y el cero de $x-3$ (divisor).

Los números representados en la segunda fila se obtienen de la siguiente forma:
12 es el producto de 4 y 3
45 es el producto de 15 y 3
120 es el producto de 40 y 3
Los números representados en la tercera fila se obtienen de la siguiente forma:
4 es el coeficiente de $x^3$ en $P(x)$
15 es la suma de 3 y 12
40 es la suma de -5 y 45
122 es la suma de 2 y 120
Ejemplo:
Sean $P(x)$ y $Q(x)$ polinomios tales que: $P(x) = -8x^3+x^4-16+2x; \, \, \, Q(x) = x-8$.
Usando división sintética, determine el cociente y el residuo $R(x)$ que se obtiene al dividir $P(x)$ por $Q(x)$.

Solución:

Ordenando $P(x)$ en forma desendiente de acuerdo a su grado, se obtiene:
$P(x) = x^4-8x^3+0x^2+2x-16$, y realizando la división se tiene:



Los números 1, 0, 0 y 2 son coeficientes del cociente. Y el número 0 es el residuo.
Por lo que $C(x) = x^3+0x^2+2x-16$ o sea $C(x) = x^3+2$ y
Nota: Observe que al realizar la división sintética, tanto los coeficientes del dividendo que son diferentes de cero, como los que son iguales a cero, debem escribirse.
Ejemplo:
Sean $P(x)$ y $Q(x)$ polinomios tales que: $P(x) = x^3+x$ y $Q(x) = x+4$
Usando división sintética determine el cociente $C(x)$ y $Q(x)$.
Solución:
Como $P(x) = x^3+0x^2+x+0$ y el cero $x+4$ es -4 tenemos que:

Por lo tanto el cociente que se obtiene, al dividir $P(x)$ por $Q(x)$ es $x^2-4x+17$ y el residuo es -68.
Ejercicio:

Para cada par de polinomios $A(x)$ y $B(x)$ que se definen acontinuación determine por división sintética el cociente y el residuo que se obtiene al dividir $A(x)$ por $B(x)$.



1. $A(x) = x^5-32; \, \, \, \, B(x) = x-2$
2. $A(x) = -7x^2+8x+5x^3+1; \, \, \, \, B(x) = x-3$
3. $A(x) = x^3+27; \, \, \, \, B(x) = x+3$
4. $A(x) = x^3-2-3x; \, \, \, \, B(x) = x+5$
5. $A(x) = x^4-x; \, \, \, \, B(x) = x+1$
6. $A(x) = 6-5x+4x^2; \, \, \, \, B(x) = x+2$
Ejemplo:
Sea $P(x)$ un polinomio tal que: $P(x) = x^5-3x^4+8x^2-2$; usando división sintética determine $P(-2)$ y 

Solución:

Recuerde que $P(\alpha)$ es igual al residuo que se obtiene al dividir $P(x)$ por $x-\alpha$.
Efectuando las divisiones correspondientes se tiene:


Ejercicio:

Sea $P(x)$ un polinomio tal que $P(x) = x^3-2x^2-9x+18$

Usando división sintética determine $P(1), \, \, P(2), \, \, P(-3), \, y \, P(-4)$
Publicado por en No hay comentarios:
Suscribirse a: Entradas (Atom)